Introduction

The governing equation for pressure distribution in a fluid film journal bearing is incompressible Reynolds equation which is derived from the Navier-Stokes equation, as expressed below. The fluid film forces acting on the journal are determined by application of boundary conditions and integration of pressure distribution. It is an iterative process until the convergence criterion is satisfied. Once the static equilibrium is found, the bearing static performance, such as bearing eccentricity ratio, attitude angle, minimum film thickness, maximum film pressure, frictional power loss, oil flow rate, etc., can be easily determined. Under dynamic conditions, the journal is oscillating with small amplitudes around the static equilibrium position. The eight bearing dynamic coefficients (stiffness and damping) are obtained by solving the perturbed pressure equations.

where x is in the axial direction and y is in the circumferential direction. Gx and Gy called the turbulent flow coefficients are the correctional terms of viscosity caused by the turbulent diffusion:

For laminar flow, Gx = Gy = 12. A critical parameter affected by turbulence is the shear stress acting on the shaft.

where Cf is the turbulent Couette shear stress factor. For laminar flow, Cf = 1.

The boundary conditions in the axial coordinate are that the pressure is ambient at the edges of the bearing pad. The Swift-Stieber or Reynolds boundary conditions are applied in the circumferential coordinate. Film cavitation is considered and the transition boundary curve to the film rupture is determined by iteration.

The governing equation for pressure distribution in a gas/air lubricated journal bearing is compressible Reynolds equation.

This compressible Reynolds equation is more difficult to analyze due to the existence of the pressure (P) in each terms compared with the incompressible flow, which makes the problem non-linear. Weak formulation based on variational principle is applied for generating the finite element model for the boundary value problems. Since this is a nonlinear problem, Newton-Raphson’s iterative scheme is utilized to solve the pressure increment, or pressure correction.

1. Tilting Pad Bearing Geometry

A 5-pad tilting pad journal bearing is shown schematically in the following figure. Clearances are exaggerated in the figure for illustrative purposes.

Two coordinate systems can be used in DyRoBeS©_BePerf and they are described in the Coordinate Systems Section.

The journal static equilibrium position is defined by the journal eccentricity (e) and attitude angle ( 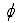). Under dynamic conditions, the journal is oscillating with small amplitudes around this equilibrium position. However, the bearing dynamic coefficients (stiffness and damping coefficients) can be calculated in any coordinate system (x,y,z) by specifying a Coefficient Coordinate Angle in the bearing input data. The Coordinate Angle is measured from the X-axis (used to describe the bearing geometry) to x-axis (used to describe the bearing coefficients). See Coefficients Coordinate Angle.

The same concept of preload described in the fixed lobe bearings applies to the tilting pad bearings. Preload is defined as the fraction of the distance between the pad center of curvature and bearing center to the pad radial clearance:

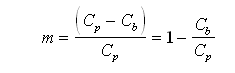
Typical preload value for a tilting pad bearing ranges from 0.15 to 0.75.

The Offset, also called Pivot Ratio, is the fraction of the distance between the leading edge and the pad pivot point to the complete pad arc length:

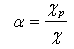
The typical pivot offset ranges from 0.50 to 0.65, i.e. the pivot point can be anywhere from one-half the length of the pad to 65 % of the pad. A pivot ratio of 0.5 is also called centrally pivoted which is suitable for either direction of shaft rotation. For better load carrying capacity, the pivot point is usually placed further than the midpoint (say offset = 0.55 ). An offset factor less than 0.5 increases the diverging film thickness and is not desirable.

Since pad arc length and pivot offset are used in tilting pad bearings instead of leading and trailing edges of the lobe described in fixed lobe bearings, the Pivot Angle (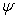) must be specified in the tilting pad bearing to define the bearing orientation and load vector direction. Pivot Angle is the angle from the Negative Load Line for Lund’s Coordinate System and from the positive X-axis for Standard Coordinate System to the first pad pivot point measured in the direction of shaft rotation. Most tilting pad bearings are designed such that the pivots are symmetrical with respect to the load vector, i.e. the load is directed onto a pad pivot or between two pivots. The Pivot Angles for Load on Pivot and Load between Pivots for the Lund’s Coordinate System are listed below:

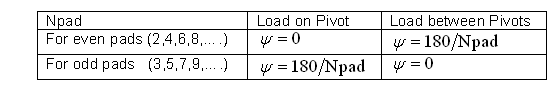
For small bearings, the pad inertia and pivot flexibility are usually neglected. For large bearings, the pad inertia and pivot flexibility can reduce the bearing effective stiffness and damping significantly. Several types of pad and pivot flexibility effect are included in the program. They are:

Rigid pivot with inertia effect

Spherical pivot – point contact

Cylindrical pivot – line contact

General curvatures

Constant stiffness